Happy New Year 2015!

The exploration of physics and math will continue in 2015. But now is a time to celebrate the new year. Happy New Year!

The Hopf Algebra

Continuing the discussion, a bialgebra is a structure which is both an algebra and a coalgebra subject to a compatibility condition. A Hopf algebra H is a bialgebra with yet another property: the antipode. The antipode is a map from H to H and is usually named S.

If the bialgebra is a graded space, then the antipode comes for free and by an abuse of notation people call bialgebras Hopf algebras.

The antipode must be compatible with the existing structures of multiplication and comultiplication and so the diagram bellow commutes.

One thing I forgot to mention last time is that the unit "u" has a dual: the counit \( \epsilon\) which maps elements from the algebra to the field \( k \). Most of the time the counit maps everything to zero and occasionally to one.

Let us verify the commutativity of the diagram with our friend \(kG \). Here the antipode is the group inverse: \( S(g) = g^{-1}\):

Start from the left side: \( g\) 

Moving up and right: \( g \rightarrow g\otimes g\) then moving to the right and down: \( g \rightarrow g\otimes g \rightarrow\ g^{-1} \otimes g \rightarrow 1_H\) 

Now move from left to right on the middle line. If \( \epsilon \) maps all elements to \(1_K \) we have:

\( g \rightarrow 1_K \rightarrow 1_H \) and the diagram commutes. 

For a graded bialgebra the antipode is given by the following explicit formula:

\( S = \sum_{n \geq 0} {(-1)}^n m^{n-1} {\pi}^{\otimes n} {\Delta}^{n-1}\)

where \( \pi = I - u \epsilon \)

Next time we will see Hopf algebra application to renormalization in quantum field theory. If you want to read about Hopf algebras, the standard book is a 1969 book "Hopf Algebras" by Moss Sweedler who is known for the so-called Sweedler notation. Personally I do not like the style of the book because you get lost into irrelevant details and miss the forest because of the trees, but it is a good reference.

Coalgebras

Last time we introduced the coproduct which is the essential ingredient of a co-algebra. How can we understand it? If we think of the product as a machine which eats two numbers and generates another one we understand the coproduct as the same machine working in reverse. A Xerox machine can be understood as a coproduct, but a coproduct can be understood not only a a cloning machine but as an action which breaks up an elements into sub-elements. For example a complex number can be decomposed into a real and an imaginary part and each of those are nothing but other kinds of complex numbers.

One funny example comes from shuffling cards: cutting a deck of cards in two is the coproduct, while putting it back together in all possible ways is the product. Renormalization techniques in quantum field theory generates coproducts. Here is a partial list of well studied mathematical examples. The coproduct is usually expressed with the symbol \( \Delta \) and the product is represented by the symbol \(m\).

The first (and most trivial) example come from group theory. Consider finite linear combinations of group elements:

\( kG = \{ \sum_{i=1}^n \alpha_i g_i | \alpha_i \in k, g_i \in G\}\)

\(\Delta g = g\otimes g\)

This is nothing but a basic cloning operation. A bit more complex example comes from polynomial rings:

\( \Delta (x^n) = \sum_{i=0}^n (n~choose~i) x^i \otimes x^j \)

\(m(x^i \otimes x^j) = x^{i+j}\)

Much fancier example come from the cohomology ring of a Lie group, or the universal enveloping algebra of a Lie algebra which gives rise to the so-called quantum groups which have major physical applications.

For now the question is: can we generate a coproduct given a product, and a product given a coproduct? The answer is rather surprising. The answer is yes in both cases for finite dimensional cases, but in general one can only generate a product given a coproduct.

Then can we have a mathematical structure which has both a product and a coproduct? If such a structure exists, it is called a bi-algebra and this respects a compatibility relation where tau is transposition of the terms in the tensor product. 

Let's take the group example. Start from the upper left corner with \( g_1 \otimes g_2\) and move it horizontally:

\(g_1 \otimes g_2 \rightarrow g_1 g_2 \rightarrow g_1 g_2 \otimes g_1 g_2\)

Then take it down, across and up and see you get the same thing meaning the diagram commutes:

\(g_1 \otimes g_2 \rightarrow g_1\otimes g_1 \otimes g_2 \otimes g_2 \rightarrow g_1\otimes g_2 \otimes g_1 \otimes g_2 \rightarrow g_1 g_2 \otimes g_1 g_2\)

Usually this kind of commutative diagram are fancy ways of expressing mathematical identities. For the polynomial ring the commutativity of the diagram means that this holds:

(m+n choose k) = sum over i, j with  i+j = k of (m choose i) (n choose j)

Also Hopf algebras are special kinds of bialgebras and no wonder they have major applications in combinatorics.

Next time we'll talk about Hopf algebras. Please stay tuned.

Fun with k-Algebras

Continuing from last time, suppose we have a bilinear map \( f\) from \(V \times W\) to \(L\) where V, W, and L are vector spaces. Then there is a universal property function \(\Phi \) from \(V \times W\)  to \(V \otimes W \) and there is a unique linear map \( g\) from \(V \otimes W\) to \(L\) such that the diagram below commutes:

               \(\Phi\)

\( V \times W \)-------> \(V \otimes W\)

    \                        |

       \                     |

           \                 |

       \(f\)    \              | \( g \)

                  \          |

                     \       |

                      _|   \/

                           \( L \)

The proof is trivial: "f" is used to define a function from the free vector space \( F (V \times W) \) to \( L \) and then we make a descent by modding by the usual equivalence relation of the tensor product to define the map \( g \).

This all looks a bit pedantic, but the point is that any multiplication rule in an algebra \( A \) is a bilinear map from \( A \times A \) to \( A\) and we can now put it in tensor formalism.

In particular consider the algebra \( A \) of matrices over a field \( k \). Matrix multiplication is associative, and we also have a unit of the algebra: the diagonal matrix with the where the elements are the identity of \( k \).  This is a prototypical example of what is called a k-algebra.

Can we formalize the associativity and the unit using the tensor product language? Indeed we can and here is the formal definition:

A k-algebra is a k-vector space \( A \) which has a linear map \(m : A\otimes A \rightarrow A\) called the multiplication and a unit \(u: k \rightarrow A \) such that the following diagrams commute:

                     \( m \otimes 1\)

\( A \otimes A \otimes A \) ----------> \(A \otimes A\)

              |                             |

              |                             |

  \( 1 \otimes m\) |                             |  \( m \)

              |                             |

              |                             |

             \/                            \/

          \(A \otimes A\)   ---------->    \(A \)

                           \( m\)

and

                          \(A \otimes A\)

                    _                    _

                      |         |         |

\( u\otimes 1\)       /              |                \ \( 1\otimes u\)

              /                 |                    \

\( k \otimes A \)                      | \(m \)               \(A \otimes k\)

              \                 |                     /

                  \              |                 /

                       _|      \/          |_

                               \( A \)

Please excuse the sloppiness of the diagrams, it is a real pain to draw them.

So what are those commuting diagrams really saying? 

The first one states that:

\( m(m (a\otimes b) \otimes c) = m(a \otimes m(b \otimes c)) \)

In other words: associativity of the multiplication: (a b) c = a (b c)

The second one defines the algebra unit:

\( u(1_k ) a = a u(1_k )\)

which means that \( u (1_k) = 1_A \)

So why do we torture ourselves with this fancy pictorial way of representing trivial properties of algebra? Because now we can do a very powerful thing: reverse the direction of all the arrows. What do get when we do that? We get a brand new concept: the coproduct. Stay tuned next time to explore the wondeful properties of this new mathematical concept.

A fresh look at the tensor product

(the very first lesson in category theory)

Recently I was reviewing Hopf algebras and their applications in physics. This is a very interesting and straightforward topic on par with linear algebra which students learn in first year in college, but unfortunately not well known in the physics community. Starting with this post I will present a gentle introduction and motivation and we'll get all the way to the application in renormalization theory for quantum field theory.

The place to start is to understand what a tensor product really is. In physics one encounters tensors every step of the way and the usual drill is about covariant and contravariant tensors, but this is not what tensors are about. 

We want to start with two vector spaces V and W over the real numbers and attempt to combine them, The easiest way to do that is to have the cartesian product VxW which are the pairs of elements (v, w) each of them in their vector space. If those spaces are finite dimensional, say of dimensions m and n, what is the dimension of VxW? The dimension is m+n but we want to combine them in a tighter way such that the resulting object dimension is m*n not m+n. How can we get from the Cartesian product to the tensor product?

The mathematical answer is a bit dry so let's simply state it. We start with a free vector space over out field or real numbers F(V) and this is nothing but formal sums of elements in V such as:

\(\alpha_1 v_1 + \alpha_2 v_2 + \cdots \alpha_n v_n\)

with \(\alpha_i \in R\) and \(v_i\) in V.

Then of course we can consider F(VxW) and now let's ask what the dimension of this object is? Its dimension equals the number of elements in VxW which is infinite and so we constructed a big monstrosity. We want the dimension of the tensor product to be m*n so to get from \( F(V \times W)\) to \(V\otimes W\) we want to cut down the dimension of \( F(V \times W)\) by using appropriate equivalence relations which capture the usual behavior of tensor products.

To recap, we started with \(V \times W\) but this is too small. We expand it to \(F(V\times W)\) but this is too big, and now we'll cut it down to "Goldilocks" size by equivalence relations.

What are the properties of \(v\otimes w\)? Not too many:

• \(\lambda (v\otimes w) = (\lambda v)\otimes w\)
• \(\lambda (v\otimes w) = v\otimes (\lambda w)\)
• \(v_1\otimes w + v_2\otimes w = (v_1 + v_2)\otimes w\)
• \(v\otimes w_1 + v\otimes w_2 = v\otimes (w_1 + w_2 )\)

Then \(F(V\times W) \) modulo the equivalence relationship above is the one and only tensor product: \(V\otimes W\) with dimension m*n.

So what? What is the big deal? Stay tuned for next time when this humble tensor product will transform the way we look at products in general. 

The Quantum Cheshire Cat

Before I begin let me reveal the answer for the last post. If no skipping is allowed, the best strategy can achieve 50%. However when not answering is an option, the maximum win rate now jumps to 75%!!!. Here is the original source of the puzzle: http://www.relisoft.com/Science/hats.html where the problem was put in terms of hats. The full answer is here: http://www.relisoft.com/Science/hats3.html and please open it only after fully giving up trying to solve the problem yourself.

Now back to today's topic. Schrodinger's cat is sooo... last century. Meet the Cheshire Cat from Alice in Wonderland:

‘All right,’ said the Cat; and this time it vanished quite slowly, beginning with the end of the tail, and ending with the grin, which remained some time after the rest of it had gone.

‘Well! I’ve often seen a cat without a grin,’ thought Alice, ’but a grin without a cat! It’s the most curious thing I ever saw in my life!’

Can this be even possible? Well,... quantum mechanics is stranger than common sense and indeed it is "possible". To understand how this works, please read this clearly written paper: http://arxiv.org/pdf/1202.0631v2.pdf by the heavyweights: Yakir Aharonov, Sandu Popescu, Daniel Rohrlich, and Paul Skrzypczyk. 

But how can we detect part of the wavefunction? The answer is weak measurements. However, this requires many repeated measurements to extract the information. Fine, but is this real? Indeed it is, and it has been observed in an actual experiment: http://www.nature.com/ncomms/2014/140729/ncomms5492/pdf/ncomms5492.pdf

From the quantum mechanics point of view, this is all relatively trivial, but from the general public impact it has a certain "sex appeal" and this is where journals like Nature thrive. Despite the large impact factor, the intrinsic science content in such journals is rather below mediocre which prove that packaging and good marketing sells. It is important to generate excitement about science in the society at large, but if you are not careful this can easily starts the slippery slope of tabloidization.

As a case in point, the quantum Cheshire cat. Stranger things occur in an interferometer like the one above when weak measurements are involved. By adding a second interefometer in the top arm of the larger interferometer, Lev Vaidman showed that in certain cases the particle (electron, cat, etc) circulating inside the inner interferometer has no connecting paths with the outside circuit, which in effect means that it forms a causal loop. And this too is revealed by weak measurement. Unfortunately I do not have a paper reference for this, but I consider this effect more interesting than the quantum Cheshire cat. The reason the quantum Cheshire cat is now hyped by Nature and other science outlets (which are not talking about Vaidman's more interesting case) has to do with the popularity of the story of Alice in Wonderland and not with its intrinsic scientific value. 

Variations on Romanian Whist Game

Now I want to go back to quantum mechanics for a bit and what better way than by playing card games. To this day I enjoy a type of Whist game, called Romanian Whist and one variant on this is when on the one games you get a card and you place it on your forehead without looking at it. Each player can see all other player's card values, but not his own. 

So let us now imagine the following "game": there are three players, and each is dealt a card. The cards could be either red or black as below.

Each player places his/her card on his forehead and is able to see the other two player's card color but not his own. Then each player tries to guess the color of their card. The guesses are done simultaneously and independently. The game is won if everyone guesses correctly. What is the best strategy which maximizes the chances of winning, and what is the maximum probability of success?

So what does this have to do with quantum mechanics? If you recall Bell's theorem, quantum mechanics is all about correlations which cannot be explained by shared randomness. But what if some measurements are allowed to be discarded? (This is called the detection loophole). Can we achieve higher correlations?

So now in the game above let's change the rules a bit: each player is allowed to enter a guess or abstain. The game is won if at least one person makes a correct guess and there are no incorrect guesses. What is the maximum possible chance of winning the game under the detection loophole variant?

Let us summarize the questions:

1. What is the best strategy and what is the maximum chance of winning the game when everyone is forced to take a guess?
2. What is the best strategy and what is the maximum chance of winning the game when you are allowed the freedom to answer or not?

I got this problem from the internet and I will not reveal the source this time because they also have the solution. Do not try to search for it because I restated it on purpose to prevent spoiling the fun of solving it, but I will give full credits next time. You will be surprised to find out just how much better the odds become when skipping an answer is allowed.

Understanding the Standard Model

Today I want to talk high level about the Standard Model and try to extract its insights. The Standard Model is basically quantum field theory and there are excellent books available on the topic. Personally I learned QED long ago from Mandl and Shaw – an excellently balanced and clear introductory textbook (I never read the second edition). If you want to really understand what is going on and not miss the forest because of the trees, an outstanding book is Zee’s "Quantum Field Theory in a nutshell” (maybe in a watermelon-the book has 518 pages). However, I do not recommend it as a first book but read it only after reading the first 10 chapters of Mandl and Shaw. For the serious practitioner earning a living computing Feynman diagrams, Peskin and Schroeder is the gold reference.

Mathematically, the basic idea is that of fiber bundles: just think of them as a common rug. However, Zee has a much better pictorial representation for physicists: consider the space-time like a giant mattress. Jump on it and you create a particle (excitation) at that coordinate. Of course you have bosons and fermions. Let's discuss the simplest case: the electron and electromagnetism. Let's forget about spin and spinors for the moment. The probability to detect the electron is given by the quantum wavefunction which is attaches a complex value at each space-time point. All expectation values are insensitive to an overall complex number phase, and by Noether theorem, invariance under this symmetry implies a law of conservation: the charge is conserved. Now let's add relativity which demands that signals cannot go faster than the speed of light. However this is at odds with the uncertainty principle and the way out is to go to second quantization which demands pair production of particles and anti-particles. If the global symmetry is changed into a local symmetry, we get to the idea of fiber bundles and local phase changes demand an adjustment in computing derivations. In other words we have what mathematicians call a connection and physicists call a potential. The potential turns out to be a vector potential \(A_\mu \) and this is the electromagnetic potential. Upon quantization, the picture now becomes that of Feynman diagrams: the vector potential which comes from a local phase mismatch between neighboring points is now a virtual photon in Feynman diagram.

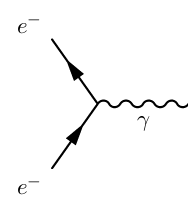
So this is the basic idea. One more thing I learned in graduate school is that such diagrams were known before Feynman, but they were not computed relativistically. Feynman major contribution was to compute them relativistically which introduced about an order of magnitude overall simplification in their computation. As an apocryphal story, Feynman once attended a physics conference where someone presented the result of six month of computation using non-relativistic diagrams which Feynman managed to double check in thirty minutes using his method and found a mistake. 

Now electromagnetism is known to be invariant under gauge transformations, and the way you couple the electron to the photon (known as minimal coupling) preserves this gauge invariance. 

So far so good, electromagnetism is an interaction based on exchanging a particle (a virtual photon) and since the photon is massless, the range of the interaction is infinite. How about the other interactions? It turns out all other interactions are basically the same thing and electromagnetism generalizes into Yang-Mills gauge interactions. Here is how is done: In quantum mechanics there is a 1-to-1 correspondence between observables and generators. Observables are hermitian operators which obey a Jordan algebras, while generators are anti-Hermitean operators which obey a Lie algebra. From generators of Lie algebras one constructs by exponentiation a Lie group and in this case we are talking about \( SU(n) \). Q: how many generators are for \( SU(n) \)?  A: \(n^2 - 1\). For electromagnetism the gauge group is \( U(1) \) which has elements of the form \( e^{i \phi} \), the weak force has three generators (the Pauli matrices), and the strong force has eight generators. 

The generators correspond in second quantization to emission and absorption of one quanta of interaction (photon, W+, W-, Z, 8 gluons) and they are 4-vectors just like \( A_\mu \). The key difference between electromagnetism and Yang-Mills is that the generators do not commute. Why? Expressed them as matrices: \( A_\mu = (A_0, A_x, A_y, A_z ) \) where each \(A \)  is a \( n \times n\) matrix. Physically this means that they carry "charge". In electromagnetism there is only one electric charge, in weak interaction there are two charges (which mixes electrons with neutrinos and up quarks with down quarks), and in the strong  interaction there are three charges (red, green, and blue). Alternatively, an electron or a neutrino is the same physical particle which becomes an electron or a nutrino upon measurement just like an electron has a spin which becomes up or down when passed through a Stern-Gerlach device. Because the field lines carry charge, unlike in electromagnetism, for two charges in the \( SU(3) \) and higher hypothetical \( SU(n>3)\) cases the field lines are parallel because it is energetically more advantageous. What this meas is that quarks cannot be free because separating them adds energy to the point where two more quark-antiquark particles are formed in the middle. For the strong interaction the only possible states which are allowed in nature are the singlet state of zero color charge, all other states requiring an infinite amount of energy to be created. For \(SU(3)\) there are only two possible singlet color states corresponding to 3 or 2 quarks (proton, neutron for 3 quarks, mesons for 2 quarks). 

The gauge group of the Standard Model is \(U(1)\times SU(2) \times SU(3) \) which means that the following particles are possible:

\(up_{r} ~~~ down_{r}\)

\(up_{g} ~~~ down_{g}\)

\(up_{b} ~~~ down_{b}\)

\(e ~~~ \nu\)

The strong force mixes the top three rows, while the weak force mixes the two columns. The particles here form what is called a "family". There are two more families identical from the point of view of gauge symmetries, but different in mass (heavier). The origin of the families is unknown and a possible explanation comes from string theory. 

Now all the particles (photon, Ws, Z. gluons, electrons, neutrinos, quarks) are massless or nearly massless (compared with the energy level at the unification scale which is the natural energy).  

Adding mass to photons, Ws, Z, gluons in the Lagrangian spoils gauge invariance, but this can be restored if it is part of another field called the Higgs field. How does this work? A zero mass particle, just like the photon has two degrees of freedom corresponding to two perpendicular modes of oscillation (two polarizations). Making a massless particle into a massive one adds a longitudinal degree of freedom which must come from some other field. If you recall the "Mexican Hat potential", a Higgs field has two modes of oscillation: radially (corresponding to the Higgs particle) and circular corresponding to a massless Goldstone boson. The Goldstone boson combines with a massless particle like W and gives rise to a massive W. This is why W and Z particles are massive and because of it particle decay is relatively slow. How do particle decay? Take a heavy quark-antiquark combination, they form a W particle in a mechanism similar with vacuum polarization is QED and then W decays into a lighter combination of electron and antineutrino. 

The Higgs mechanism works only for W+, W-, and Z, not for photons or gluons. There are two more twists in the Higgs process. First, this mechanism breaks the symmetry but the singlet boson mixes with the electromagnetism boson and results in the massive Z and the massless photon. The photon is not really the photon before symmetry breaking! Second, how do the fermions acquire mass?

Fermions interact with other fermions through the minimal coupling from above. However, they also couple with the Higgs field by "Yukawa coupling" and this is how they get mass. Fermion masses has to do with the fact that in nature the mirror symmetry is broken. Left handed particle behave differently than right handed particle in weak interaction. If you look at Dirac's equation and write it in terms of left handed and right handed components, the fermion propagation mixes them up. Without Yukawa coupling for fermions the left-handed physics would have been completely equivalent with right handed physics. What happens is that Dirac's equation is valid only in the approximation that the Higgs field does not excite radial oscillations and the mass of the fermions depend on the radial value of the Mexican Hat potential at the minima and the coupling coefficient.

Now if the Higgs Mexican hat potential would have had a different minima, or if the Yukawa coupling would have been different, then our universe would have looked completely different. Take the up and down quark masses for example. If those masses would have been the other way around, then the neutron would have been stable and the proton would have decayed into it preventing the formation of atoms. Chemistry and life would have been impossible. 

Our universe is the way it is because we are trapped in a local energy minima. What generates this minima? Can an ant walking on the surface of an apple understand the concept of the apple and how it got there? I think one of the triumphs of string theory is actually predicting the landscape of local minima despite the criticism of the lack of predictive power. This is the Copernican principle in action. We are in no way special. The Earth is one of the planets of the solar system, the Sun is one of the 100 billion stars in out galaxy, the Milky Way is one of the 100 billion known galaxies, and probably our universe is one of the  \( 10^{100}\) possible local energy minima each with very different particles then the ones in our universe. Quantum mechanics "multiverse" (from MWI) is almost sure gobbledygook, but eternal inflation, bubble universes, and the multiverse landscape are almost surely real.

Clothes for the Standard Model beggar

Although there were several other interesting talks at the DICE2014 conference, I'll not talk about them because they are right in my active research area and I do not want to present half-baked ideas and work in progress.

One very interesting talk was given by Fields Medal winner Alain Connes:

I won't talk about this because I do not fully understand it (and him pulling a Houdini-type disappearance after the talk like all the 100+ physicists at the conference were infected with Ebola prevented the opportunity to ask in depth questions). But I do want to present some general ideas about Connes-Chamseddine approach to the Standard Model which occurs naturally in Connes' non-commutative geometry setting.

Now when you look at the action for both general relativity and the standard model you notice the groups of invariances. In general relativity you have the group of diffeomorphims, and in the Standard Model you have the group of gauge transformations. Diffeomorphisms are easy to understand because they mean that there is no preferred system of reference in nature. One way to unify of gravity with Standard Model is to try to understand diffeomorphism as a gauge group. This is a faulty interpretation and Streater talks about it in his famous "lost causes". Now Connes' idea is the other way around: we can obtain the gauge group from diffeomorphism in a suitable generalized space. And so Connes' unification is geometrical in nature.

To get to the full Standard Model is not at all easy and is best to see how all this works on a toy model: gravity coupled with SU(n) Yang Mills theory. Start with a manifold M and consider continuous functions on it: \( C^{\infty} (M) \). Now let's add at each point an internal space described by an \( n \times n\) complex matrix representing the inner degrees of freedom of a Yang-Mills theory. Then consider the involutive algebra \( A\) of \( n \times n\) matrices of smooth functions on the manifold M:

\( A = C^{\infty} (M, M_n (C)) = C^{\infty} \otimes M_n (C)\)

Now the fireworks: the inner automorphism \( Inn (A) \) is isomorphic with the gauge group \( \mathcal{G}\) and the short exact sequence:

\( 1 \rightarrow Inn (A) \rightarrow Aut(A) \rightarrow Out(A) \rightarrow 1\)

is equivalent with:

\( 1 \rightarrow \mathcal{G} = Map(M, U(n)) \rightarrow Diff(X) \rightarrow Diff(M) \rightarrow 1\)

And so the full group of invariance on a new space \( X = M \times M_n (C) \) is the semidirect product of the diffeomorphisms on M with the gauge group and the diffeomorphism shuffles (acts on) the group of gauge transformations.

Generalizing the space from a regular manifold to a product of the manifold with a discrete non-commutative space F: \(X = M \times F\) by pure geometrical concept of diffeomorphism in the new space generates general relativity coupled with new gauge degrees of freedom which can be understood as inner fluctuations of the metric. 

Now for the connection with non-commutative geometry: because in nature there is no absolute coordinate system, to specify a position one needs to use geometric invariants, and in particular, there is an alternative description of them using spectral information. Connes makes the point that the very definition of a meter now uses a certain laser wavelength information-a spectral concept. From non-commutative geometry Connes introduced a spectral triple (A, H, D) where A is an algebra, H is a Hilbert space, and D is Dirac's operator to have an alternative encoding of the geometric information in a diffeomorphic setting. For the Standard Model the job was to find an appropriate spectral triple which will generate the Einstein-Hilbert action of general relativity and the Standard Model action.

And so for the Standard Model beggar its clothes come as follows: the algebra A comes from the gauge group information, the Hilbert space comes from fermions and a spin manifold, and the Dirac operator comes from the Yukawa coupling matrix. In the end, while the new equivalent description does represent a simplification, the algebra \( A \) is rather complex as it involves the three generations of matter and the full theory is not as neat as the toy model.  One last key point: how can we define the notion of distance in a space which contains a discrete space? In non-commutative geometry there is a suitable generalization using the norm of an operator which works even for discrete spaces.  

Much more can be said about this approach to the Standard Model, but I only wanted to present a 10,000 feet impressionistic view of it. I only want to state one more thing: Connes-Chamseddine approach predicts new physics beyond the Standard Model and rejects the "big desert hypothesis" in order to correctly predict the Higgs mass and so the theory is falsifiable. 

Clever integration tricks

Today I want to talk about a clever integration trick I learned from Achim Kempf at DICE2014. Any mathematical physicist learns clever integration tricks and one of my personal favorite is how to compute:

\(I = \int_{-\infty}^{+ \infty} e^{-x^2} dx \) 

because there is no elementary primitive function since the integral comes from the Gaussian (normal) distribution. However one can still compute the integral above quite easily by going to a 2-dimensional plane and considering the \( y \) integral as well: \(\int_{-\infty}^{+ \infty} e^{-y^2} dy \) which is \( I\) again .

So 

\(I ^2 = \int_{-\infty}^{+ \infty}\int_{-\infty}^{+ \infty} e^{-x^2} e^{-y^2} dx dy  = \int_{-\infty}^{+ \infty}\int_{-\infty}^{+ \infty} e^{-(x^2 + y^2)} dx dy \)

and the trick is to change this to polar coordinates:

\( x^2 + y^2 = r^2\) and \( dx dy = rdr d\theta\)

integration by \( \theta\) is a trivial \( 2 \pi\), and the additional \( r \) allows you to find the primitive and integrate from \(0 \) to \( \infty\).

But how about not having to find a primitive at all? Then one can try Achim's formula:

\( \int_{\infty}^{\infty} f(x) dx = 2 \pi f(-i\partial_x ) \delta (x) |_{x=0}\)

It's a bit scary looking

Happy Halloween!

but let's first prove it:

\( 2 \pi f(-i \partial_x) \delta(x) |_{x = 0} = f(-i \partial_x)  \int_{-\infty}^{+\infty} e^{ixy} dy |_{x = 0}\)

due to a representation of \( \delta (x)\):

\( \delta (x) = \frac{1}{2 \pi} \int_{-\infty}^{+\infty} e^{ixy} dy \)

Moving \( f(-i \partial_x) \) inside the integral makes this \( \int_{-\infty}^{+\infty} f(y) e^{ixy} dy |_{x = 0} \). Why? Expand \( f \) in Taylor series and apply the powers of \( -i \partial_x \) on \( e^{ixy} \) resulting into the powers of \( y \). Then recombine the Taylor series terms in \(f(y) \). Finally compute this for \( x = 0 \) which kills the exponential term and you are left only with \( \int_{-\infty}^{+\infty} f(y) dy\) and the formula is proved.

So now let's see this formula in action. Let's compute this:\( \int_{-\infty }^{+\infty} \frac{sin x}{x} dx\):

\( \int_{-\infty }^{+\infty} \frac{sin x}{x} dx = 2 \pi sin(-i \partial_x) \frac{1}{-i\partial_x} \delta(x) |_{x = 0} = \)

\( = \frac{2 \pi}{-i} \frac{1}{2i} (e^{\partial_x} - e^{-\partial_x}) (\theta(x) + \epsilon) |_{x = 0}\)

Now we can use Taylor to prove that \( e^{a \partial_x} f(x) = f(x+a) \) and from this the integral becomes:

\( = \pi (\theta(x+1) - \theta(x-1) +c - c)|_{x=0} = \pi (1 - 0 + 0) = \pi\)

So what is really going on in this formula? If we start with another representation for the Dirac delta:

\( \delta(x) = \lim_{\sigma \rightarrow 0^{+}} \frac{1}{\sqrt{\pi \sigma}} e^{-\frac{x^2}{\sigma}}\)

then:

\(\int_{-\infty}^{+\infty} f(x) dx = \lim_{\sigma \rightarrow 0^{+}} 2 \sqrt{\frac{\pi}{\sigma}} e^{\frac{{\partial_x}^2}{\sigma}} f(x) |_{x=0}\)

The exponential term is a Gaussian blurring which flattens \( f(x) \), and is in fact a heat kernel because a heat equation is actually a convolution with a Gaussian. Also the limit sigma goes to zero or equivalently one over square root of sigma goes to infinity would physically correspond to the temperature going to zero. 

However something does look fishy in the formula. How can the integral of a function which includes the values over the entire domain be identical with a a formula containing only the value of \( f\) in only one point \( x = 0\) ? It does not! This is because \( e^{\frac{\partial_{x}^{2}}{\sigma}}\) acts nonlocally because \( e^{\frac{\partial_{x}^{2}}{\sigma}}f(x) \) is a convolution! 

More can be said, but it is a pain to typeset the equations and the interested reader should read http://arxiv.org/abs/1404.0747. Enjoy.

­Should Gravity be Quantized?

Merging quantum mechanics with general relativity is the hardest problem of modern physics. In naive quantum field theory, treating gravity quantum mechanically involves adding smaller and smaller distance contributions to perturbation theory but this corresponds to higher and higher energy scales and adding enough energy will eventually lead to creating a black hole and the overall computation ends up predicting infinities. String theory, loop quantum gravity, and non-commutative geometry have different ways to deal with those infinities, but there are also approaches which challenge the need to treat gravity using quantum theory. Those approaches are a minority view in the physics community and I side with the majority point of view because I know it is mathematically impossible to construct a self-consistent theory of quantum and non-quantum mechanics. But wouldn't be nice to be able to put those ideas to an experimental test?

Here is where a nice talk at DICE2014 by Dvir Kafri came in.  The talk was based on http://arxiv.org/abs/1311.4558 and http://arxiv.org/abs/1404.3214 .  The best way to explain is probably to present it from the end, and here is the proposed experiment (from http://arxiv.org/pdf/1311.4558.pdf ).

Penrose advanced the idea of the gravitational collapse of the wavefunction and Diosi refined this in the best available model so far. Rather than looking at decoherence of objects due to gravity, Dvir instead asks the following question: can two masses which only interact gravitationally become entangled? Direct superposition experiments are out of the question, but how about measuring some sort of residual quantum noise required to screen the entanglement from occurring in the first place? Sure, since the gravitational coupling is so weak, the noise needed to do this is really tiny, but what if we cool the experiment close to absolute zero? One experiment is not enough because at 10 micro Kelvins you expect one thermal phonon to be emitted every 10 seconds and the desired effect produces a phonon every 3000 seconds, but massively replicating the experiment in parallel might work to extract the signal (replicate 10,000,000 times! – OK this is a bit in the realm of science fiction for now but maybe future technological advances will drop the price of such an experiment to something manageable).

Dvir motivates the experiment by modeling how two distant objects can communicate by individually interacting with an intermediary object.

Here is a slide picture from Dvir’s presentation (I thank Dvir for providing me with a copy of his presentation)

Please note that position and momenta are non-commuting operators. So you apply A first, followed by B, followed by –A and the by –B. The intermediary F (a harmonic oscillator) is unchanged by this procedure, but gains a geometric phase proportional to \( A \otimes B \). In other words this is what happens:

If you break this process into n infinitesimal steps and repeat n times, by a corollary of Baker-Campbell-Hausdorff formula you get:

\( {(t/n)}^{n} = exp (-it [H_A + H_B + A\otimes B]) \)

This picture is a simple model for how two objects can become entangled, To prevent that entanglement (but still allow communication between A and B), we add a “screen” S  which captures the coupling with the environment

By the monogamy of entanglement, this can only decrease the entanglement between A and B.

Since the environment is learning about A and B through F, Dvir invokes what he calls the “Observer Effect”: a measurement of observable \( O \) necessarily adds uncertainty to an non-commuting observable \( O^{’} \). In this case, the process of screening entanglement means that all observables not commuting with A and B become noisier.

Here is an experimental setup that is analogous to the first experiment: S is a weak measurement and the purpose is to see the noise generation, which is model-independent in that the equations of motion are the same.

If a certain inequality is violated (relating the strenght \( \eta \) of the \( A \otimes B \) interaction to the noise added to the system), then the communication channel between the Alice-Bob system transmits quantum information. Analogously, if we can verify that \( \eta \) is only due to gravity (that is why there is a superconductor shield between the oscillators coupled by gravitational attraction), by observing the noise and checking the inequality we can conclude that gravity can convey quantum information. Pretty neat.

PS: I thank Dvir for providing clarifying edits to this post.

The amazing Graphene

Continuing the interesting talks series from DICE2014, I was blown away by a talk by Alfredo Iorio: “What after CERN?”. Physics is an experimental science and the lack of experiments forces theoreticians to construct alternative models which most likely have nothing to do with how nature really is.

In high energy physics the experiments are extremely expensive and the price tag for a new accelerator is in the billions. Why do people need larger accelerators? Because to probe smaller and smaller regions of space you need larger and larger energies. Accelerators circulate a beam of particles in a circle to gain the required energy, and the faster they go (closer and closer to the speed of light), the heavier the particle become and they need larger and larger circle radius. To probe at the scales of the string theory for example, one needs an accelerator the size of the galaxy. So is there an alternative to this?

It turns out that there are theoretical and experimental efforts of outstanding value circumventing this brute force approach and Iorio’s research belongs into this rare breed in physics.

In the past I was blogging at FQXi about an experiment done by Bill Unruh with a laboratory waterfall which was able in principle to simulate a black hole and its Hawking radiation. However even more amazing things can be achieved with Graphene

So what is so special about this material? There are two key properties which makes it extremely interesting.

First, the hexagonal structure requires two translations to reach any atom.

Given an origin, any atom can be specified first by a linear combination of two vectors: \( (a_1 , a_2 )\): \( x_a = n_1 a_1 + n_2 a_2\) where \( n_1 , n_2\) are positive or negative integers, followed by a second translation using the vectors \( s_1 , s_2 , s_3\).

Second, the band structure in graphene is very special: the conductivity and valence band touch in exactly one point (called the Dirac point) making the structure a semi-metal:

Graphene Band

When the excitation energy is small (~ 10 \( \mu \) eV), the quasi-particle excitations respect Dirac’s equation. Two of the 4 spinor components come from the Lattice A vs. Lattice B, and the other two come from the up and down bands touching at the Dirac point.

By its very geometrical structure, graphene is an ideal simulator of spin ½ particles.

Now the hard work begins. How can we use this to obtain answers about quantum field theory in curved space-time? First we can start easy and consider defects in the hexagonal pattern. A defect changes the Euler number and introduces curvature. This is tractable mathematically for all simple defects using a bit of advanced geometry, but you don’t get very far except in the description of the phenomena in terms of critical charges and magnetic fluxes.

But if you can manufacture surfaces of negative curvature:

called Beltrami spheres then the real fireworks begins. Under the right conditions you can simulate the Unruh effect (http://arxiv.org/pdf/1308.0265.pdf ): an observer in A sees the quantum vacuum in the frame B as a condensate of A-particles. To observe this the tip of a Scanning Tunneling Microscope is moved across the graphene surface and probes the graphene quasi-particles.

More amazing things are possible like: Rindler, de Sitter, BTZ black hole, Hawking radiation.

Of course there are drawbacks/roadblocks too: the defects in manufacturing which might spoil those effects. It is unclear how accurate are manufacturing techniques at this time. Also I don’t know if the impurities effects are properly computed. Much more serious I am skeptical of the ability to maintain the hexagonal pattern while creating the Beltrami funnel. And if this is not maintained, in turn it will affect the band structure which can ruin the validity quasi-particle model of Dirac’s equation.

I brought my concerns to Alfredo and his response put my mind to ease. To avoid playing telephone, with his permission I am sharing his answer here:

“- So, you are perfectly correct when you doubt that the Beltrami shape can be done all with hexagons. In fact, this is not possible, not because of technical inabilities of manufacturers, but because of the Euler theorem of topology.

- How do we cope with that? Although at the location of the defects the Dirac structure is modified, the hexagonal structure resists in all the other places. When the number of atoms N is big enough, one can safely assume that the overall hexagonal structure dominates (even when the defects start growing, as they do with N, all they do is to distribute curvature more evenly over the surface).

Now, if you stay at small \( \lambda \) (large energy E), you see all local effects of having defects, and the lattice structure cannot be efficiently described by a smooth effective metric (essentially, since the \( \lambda \) and E we talk about here are those of the conductivity (or \( \pi \) ) electrons that live on the lattice (they don't make the lattice, that is made by other electrons, belonging to the \( \sigma \) bonds), we realize that when their wavelength is big enough, they cannot see the local structure of the lattice, just like large waves in the sea are insensitive to small rocks. Hence, for those electrons, the defects cannot play a local role, but, of course they keep playing a global, i.e., topological, role, e.g., by giving the intrinsic curvature (as well known, in 2 dimensions the Gauss-Bonnet theorem links topology and geometry: Total Curvature = 2 \( \pi \) Euler Characteristic).

- Thus, if I was good enough at explaining the previous points, you should see that the limit for big \( r \) (that is small curvature \( K = \pm 1/r^2 \)) is going in the right direction, in all respects: 1. the number of atoms N grows; 2. the energy \( E_r \sim 1/r \) (see Fig. Graphene Band) gets small, hence the \( \lambda \) involved gets big, hence 3. the continuous metric \( g_{\mu \nu} \) well describes the membrane; 4. the overall Dirac structure is modified, but not destroyed, and, the deformations are given by a ''gauge field'', that is of the fully geometric kind. Indeed, this gauge field describes deformations of the membrane, as seen by the Dirac quasi-particles. The result is a Dirac field (we are in the continuum) in a curved spacetime (i.e. covariant derivatives of the diffeo kind appear). In arXiv:1308.0265 we discuss all of this in Section 2.

- There is also an extra (lucky!) bonus in going to big \( r \), that is the reaching of some sort of horizon (more precisely, that is a conformal Killing horizon, that, for a Hawking kind of phenomenon, is more than enough). Why so? The issue here brings in the negative curvature. In that case the spacetime (the 2+1 dimensional spacetime!) is conformal (Weyl related) to a spacetimes with an horizon (Rindler, deSitter, BTZ). Something that does not happen for the positive curvature, the sphere, that in graphene is a fullerene-like structure. In fact, the latter spacetime is conformal (Weyl related) to an Anti deSitter, that, notoriously, does not have an intrinsic horizon.

Now, once you learn that, you also learn that surfaces of constant negative Gaussian curvature have to stop somewhere in space (they have boundaries). That is a theorem by Hilbert. For small \( r \) (large curvature) they stop too early to reach the would-be-horizon. For large \( r \), though, they manage to reach the horizon. Fortunately, for that to happen, \( r \) needs not be 1 km (that would not be an impossible Gedanken experiment, but still a tremendous task, and just unfeasible for a computer). The job is done by \( r = 1 \) micron! That is something that made us very happy: the task is within reach. It is still hard for the actual manufacturing of graphene, but, let me say, it turned into a problem at the border between engineering and applied physics, i.e. it is no longer a fundamental problem, like, e.g., the mentioned galaxy-size accelerator.

- We are actively working on the latter, as well. In this respect, we are lucky that these ``wonders’’ are happening (well... predicted to be happening) on a material that is, in its own right, enormously interesting for the condense matter friends, hence there is quite a lot of expertise around on how to manage a variety of cases. Nonetheless, you need someone willing to probe Hawking phenomena on graphene, while the standard cond-mat agenda is of a different kind. Insisting, though, very recently I managed to convince a composite group of condensed matter colleagues, mechanical engineers, and computer simulations wizards, to join me in this enterprise. So, now we are moving the first steps towards having a laboratory that is fully dedicated to capture fundamental physics predictions in an indirect way, i.e. on an analog system.

What we are doing right now, between Prague, Czech Republic (where I am based) and Trento, Italy (where the ``experimentalists`` are sitting), is the following:

First, we use ideal situations, i.e. computer simulations, hence we have no impurities nor substrates here. There no mention is made of any QFT in curved space model. We only tell the system that those are Carbon atoms, use QM to compute the orbitals and all the relevant quantified, perform the tight binding kind of calculations. Thus, the whole machinery here runs without knowing that we want it to behave as a kind of black hole.

What we are first trying is to obtain a clear picture of what happens to a bunch of particles, interacting via a simplified potential, e.g., a Lennard-Jones potential, constrained on the Beltrami. This will tell us a lot of things, because we know (from similar work with the sphere, that goes under the name of generalized Thomson problem, see, e.g., the nice work by Bowick, Nelson and Travesset) that defects will form more and more, and their spatial arrangements are highly non trivial.

When this is clear, we want to get to a point where we tell the machine that we have N points, and she (the machine) plots the Beltrami of those points. i.e. it finds the minimum, the defects, etc. This would be the end of what we are calling: Simulation Box 1 (SB1).

When SB1 is up and running, we fix a N that is of the order of 3000, take away points interacting with Lennard Jones, and substitute them with Carbon atom, i.e. we stick in the data of Carbon, the interaction potential among them, and then let a Density Functional computation go. The latter is highly demanding, computer-time wise, but doable. With this we shall refine various details of the theory, look into the structure of the electronic local density of states (LDOS), although the \( r \) we can get with N = 3000 is still too small for any Hawking anything. That is the first half of SB2.

The work of SB1 and first half of SB2, can be done with existing machines and well tested algorithms. But we need to go further, towards a big \( r \) (the 1 micron at least... although I would be happier with 1 mm, but don't tell my experimentalist friends, they would kill me!). This is possible, but we are going into the realm of non tested algorithms, of dedicated machines (i.e. large supercomputers, etc). Nonetheless, figures of the order of N = 100K (and even whispered N = 1 million) are in the air. That would be second half of SB2, i.e. when the Hawking should be visible.

That is the road I can take with the current group of people involved. I don't give up though the idea of getting someone to actually do the real graphene thing. But this would only mean a handle of a very large number of points, to the expense of more impurities, substrates, etc. Indeed, the SB2 (the computer simulations of true Carbon interactions) would be so accurate, that myself (and, most importantly, the cond-mat community) would take those results as good (if not better, because `fully clean`) as the experiments.”

In conclusion this is an extremely exciting research direction. 

The topological structure of big data

One interesting talk at DICE2014 was a talk by Mario Rasetti on understanding the bid data of our age.

You may wonder what does this have to do with physics, but please let me explain. First when we say big data, what are we really talking about? The number of cataloged stellar object is \( 10^{21}\). Pretty big, right? But consider this: in 2013 there were 300 billions email sent, 25 billions SMS messages made money for phone companies, 500 million pictures were uploaded on Facebook. In total from those activities mankind produced in 2013 \( 10^{21}\) bytes. And the every year we produce more and more data. 

How much is \( 10^{21}\) bytes? How about 323 billion copies of War and Peace. Or 4 million copies of all of Library of Congress. In four years it is estimated that we will produce \( 10^{24}\) bytes which is larger than Avogadro's number!

Now how can we get from data to information to knowledge and then wisdom? From computer science we know to lay all this data sequentially and people considered vector spaces for this. But does this make sense? For example, if we take a social network like Twitter what we have are simplicial complexes. What Mario Rasetti proposed was to extract the topological information from those kinds of large data sets. In particular he computes the Homology groups and Betti numbers which were discussed on this blog on prior posts, and the reason is that the algorithmic complexity is polynomial in computation time.

We know that if we triangulate a manifold and omit one point we obtain different topological invariants just like puncturing a three dimensional balloon results in a two dimensional surface. Therefore in computing the Betti numbers we get fluctuations but as more and more nodes are included into computation the fluctuations stabilize. 

The link with physics and Sorkin's Causal Set theory is obvious and the same techniques can be applied there. However Rasetti did not go into this direction and instead he cited the application of the method to biology. In particular, he was able to clearly distinguish if a patient took a specific drug vs. a placebo from the analysis of the brain MRI image which looked identical to the naked eye. 

Recently I saw an article on what Facebook sees in posting patterns when we fall in love:

Now all this looks really scary. Imagine the power of information gathering and topological data mining in the hands of (bad) governments around the world. And not only governments. Big companies like Facebook are abusing the trust of their users and perform unconscionable sociological tests by manipulating advertising for example. In the biological area, human cloning is rejected because the general population understands the risks, but the understanding of big data and the ability to mine it for correlations and knowledge is badly lagging behind the current technical ability. More violation of privacy scandals will occur before the public opinion will put pressure to curb bad behavior of abusers of trust.

History of Electroweak Symmetry Breaking

The first post about DICE2014 is about Tom Kibble's keynote lecture about electroweak theory.

Physics in the 50s had great success with quantum electrodynamics and its perturbative methods because the coupling constant was smaller than 1: 1/137. However, for other interactions, perturbation theory was not working due to interaction strength and people looked at alternative theories, like S-matrix and Regge poles which ultimately lead to dead ends in physics.

If you look at strong interactions, the proton and the neutron are very similar and people naturally looked at the SU(2) symmetry. However this symmetry is broken by electromagnetism and people started thinking about how to break symmetries. Also from strong interactions the SU(3) symmetry was developed by Gell-Mann's eightfold way which made a successful prediction for a new particle. Today we know this is an approximate symmetry which comes from up, down, and strange quarks.

In 1954 Yang and Mills had their seminal paper in gauge theory. The same result was obtained by Ronald Show, a grad student under Abdus Salam, but he only wrote it in his PhD thesis and was not taken seriously. The problem of Yang-Mills theory is that it predicts a new infinite range interaction which does not exist in nature. Adding mass to the interaction restricts the range due to uncertainty principle, but adding a mass term makes the theory non-renormalizable.

Around the same time, Fermi developed his weak interaction V-A 4-point interaction theory and Schwinger suggested in 1957 what is now called the W+, W- weak bosons.

It was known that the weak interaction violates parity and was short range and the search was on for how to introduce this into the theory.

In 1961 Glashow proposed a solution to the parity problem by mixing Z0 with W0 and proposing the SU(2)xU(1) symmetry. Salam and Windberg independently proposed the same thing in 1964, and the W mass was put in by hand.

For the mass problem responsible for the short range of the interaction, Nambu proposed spontaneous symmetry breaking in 1960. Condensed matter physics were very familiar with spontaneous symmetry breaking as the explanation for plasmons in superconductivity.

The basic idea of spontaneous symmetry breaking is that the ground state does not share the system symmetry. A typical example is a ball of water which freezes: during crystallization the rotational symmetry is lost. In quantum field theory there was the Goldstone theory with its Mexican hat potential:

The radial motion generate an effective mass term (because locally one approximate the radial motion with a parabola), but the motion around the center corresponds to a zero mass particle: the Goldstone boson. Since the Goldstone boson was not observed in nature, this was a major roadblock to adding mass to non-abelian gauge theories.

In 1964 Gerald Guralnik at Imperial College, collaborated with Walk Gilbert - a student of Abdus Salam, and a US visitor: Richard Hagen came with the idea of the Higgs mechanism to combine the massless gauge theory with the massive Goldstone boson. The same mechanism was proposed also independently by Peter Higgs/ Guralnik, Hagen, and Kibble/, and by Englert and Brout.

The problem was how to avoid the unobserved Goldstone boson. If you impose a continuity equation you get a charge by integrating the current density. However you need to consider the surface at infinity and due to relativity and microcausality in Coulomb gauge charge does not exists as a self-adjoint operator and this avoids the presence of the Goldstone boson. The key is the presence or absence of long range forces which interfere with the Goldstone theorem.

Then the electroweak unification and successes followed: Weinberg in 1967 and Salam in 1967 and 1968 proposed the electroweak theory, in  1971 't Hooft proved its renormalizability. In 1973 Z0 neutral currents were observed in CERN, and in 1983 W and Z bosons were observed in CERN as well.

70's and 80's saw the development of quantum chromodynamic based on SU(3) and the Standard model based on SU(3)xSU(2)xU(1) emerged.

After 1983 the only missing piece of the puzzle was the Higgs boson. Originally this played a minor role, the big deal was the Higgs mechanics. In 2012 the Higgs boson was confirmed experimentally and Englert and Higgs were awarded the Nobel Prize.

So what next? Grand unification of electroweak and strong force and supersymmetry (SUSY)? With SUSY the three coupling constants for electromagnetism, weak and strong force converge exactly and this is very powerful evidence. Unfortunately there is no current experimental evidence for SUSY.

Then there is a big gap between the Standard Model and M-theory/quantum gravity. To put it in perspective, strings to Standard Model is like atoms to our Solar System. Or if an atom is blown to the size of the observable universe, a string in string theory is the size of a tree on Earth.

The Sleeping Beauty Problem

I just came back from the DICE2014 conference and as I recover from the jet lag and prepare posts about the conference I'll present the last topic in the statistics mini-series, the sleeping beauty problem. Unlike the Monty Hall problem, there is no consensus on the right solution even among the experts which makes this problem that much more interesting. 

So here is the setting: Sleeping Beauty participates in an experiment. Every day she is explained the process and she is asked about the the credence (degree of belief) that a certain fair coin landed heads or tails. So what is the big deal you may ask? The coin is fair and this means that it lands heads 50% of the time, and tails 50% of the time. However, there is a clever catch. 

Whenever the sleeping beauty is put to sleep she takes an amnesia drug which erase all her prior memory. If the coins lands tails, she will be woken up Monday and Tuesday but if the coins lands heads, she will be woken up only Monday. On Wednesday the experiment ends.

So now for the majority opinion: the thirders:

To make this very clear, let's change the experiment and keep waking up the Sleeping Beauty a million time if the coin lands tails, and only once if the coin lands heads. If she is woken up on a day at random, the chances are really small that she hit the jackpot and was woken up in the one and only Monday. So being woken up more times when the coin lands tails, means that the in the original problem the credence the coin landed heads should be one third. If you play this game many times and attach a payout for the correct guess, you maximize the payout overall if your credence is one third.

Now for the opposing minority point of view: the halfers: 

On Sunday, the credence is obviously 50-50 because the coin is fair. Even the thirders agree with this. However, From Sunday to Monday, no new information is gained, therefore the credence should be unchanged and the overall credence should remain 50% throughout the experiment. If you adopt the thirder position you should explain how does the credence change if no new information is injected into the problem. 

So which position would you take? There were all sorts of approaches to convince the other side, but no-one had succeeded so far.