Joy Christian's program of achieving quantum correlations with Clifford algebras

In the last post I explained how the algebra of the projector operators cannot always be Boolean, otherwise the Hilbert space formalism of quantum mechanics is invalid. Today I will stay in the classical-quantum divide area and I'll talk about an invalid proposal by Joy Christian which generated a lot of debate (and acrimony). When I attended the Vaxjo conference people looking up my archive record saw that I have argued against this proposal and I was asked to explain why it is invalid.

The story begins with the EPR-B experiment and the derivation of the correlation

\(-a \cdot b\)

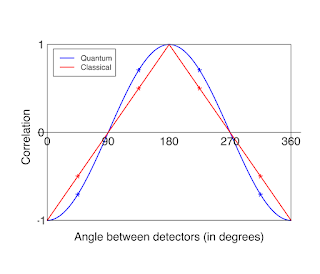
between Alice and Bob when Alice orients her detection device on direction a and Bob orients his on direction b. So the corelation curve is minus the cosine of the detection angles (the blue line below):

In this experiment the two spin 1/2 particles are in a singlet state:

\( |\Psi\rangle = \frac{1}{\sqrt{2}}( |up \rangle_{left} |down \rangle_{right} - |down \rangle_{left} |up \rangle_{right} )\)

and because the observables are \(a \cdot \sigma\) and \(b \cdot \sigma\) the correlation is:

\( \langle \Psi | (a \cdot \sigma)\otimes(b \cdot \sigma) | \Psi \rangle\)

So how can we compute this? We use an identity:

\( (a \cdot \sigma)(b \cdot \sigma) = -a\cdot b +i (a\times b) \sigma\)

which yields the final answer because \( \langle \Psi | \sigma| \Psi \rangle = 0\) as the mean value for both Alice and Bob are zero for any direction because we started with a total spin zero state (a singlet state).

Now Joy noticed this identity and thought that it would be nice if he could use it in a classical setting to recover the \(-a\cdot b \) correlation. There is a "little" problem: how to make the pesky \(i (a\times b) \sigma\) term disappear? 

So Joy came up with the following proposal: half the particle pairs obey:

\( (a \cdot \sigma)(b \cdot \sigma) = -a\cdot b +i (a\times b) \sigma\)

and the other half obey this:

\( (a \cdot \sigma)(b \cdot \sigma) = -a\cdot b -i (a\times b) \sigma\)

and so when averaged you get to the quantum correlation: \(-a \cdot b\)

But how can this be possible? It is all in the sign of \(\sqrt{-1}\) Joy claimed. When complex numbers are represented in a plane, the imaginary unit corresponds to the vertical axis. So for half of the particle pairs we draw the imaginary axis bottom up, and for the other half up bottom. But do we really get the cancellation? Nope because \(a\times b\) is a pseudo-vector which upon this reflection against the horizontal axis changes signs as well and the identity remains:

\( (a \cdot \sigma)(b \cdot \sigma) = -a\cdot b +i (a\times b) \sigma\)

and all of Joy's ill fated proposal is based on a "forgotten" -1 sign.

But if Joy would have presented his proposal like this, it would not have gotten very far. Instead Joy explained it all using the language of Clifford algebra which is not at all familiar to physicists. Also there was an associative faulty narrative about "topologically complete reasoning".

The main discovery of Joy was a no man's land at the intersection of math, physics, and philosophy: the mathematicians understanding Clifford algebra knew nothing of Bell, the physicists did not know how to counter Joy's philosophical narrative, and the philosophers had no clue of Clifford algebra. Add to this Joy's aggressive and patronizing defense of his proposal and you get a perfect storm of controversy.

The full story of debunking this nonsense would make for a nice soap opera. I was not the first who noticed the mathematical errors in Joy's proposal, I was the third out of four. Also I was not the first who wrote a paper about it, I was the second one out of three, but I was the first who uploaded it on the archive. There were other archive replies to Joy before me but nobody actually bothered to double check his math. The first reply by Marcin Pawlowski came very close to point out the problem but Joy's reply managed to discourage his critics into challenging his math:

"More specifically, the critics culminate their charge by declaring that, within my local realistic framework, it would be impossible to derive “a scalar in the RHS of the CHSH inequality. QED.” If this were true, then it would certainly be a genuine worry. With hindsight, however, it would have been perhaps better had I not left out as an exercise an explicit derivation of the CHSH inequality in Ref.[1]. Let me, therefore, try to rectify this pedagogical deficiency here."

And so people thought at that time that Joy is wrong, his physics and philosophical arguments were nonsense, but his math was correct and it was not a good idea to challenge him at that. But as it turned out all his math was only smoke and mirrors with more and more mathematical mistakes to cover up the prior ones, and I can write up an entire book about it.

All this controversy has hopefully came to an end with Joy resigning his FQXi membership, but he actually never accepted he was wrong and continues to this day to call his critics arguments: "strawmen arguments".

There was only one person who had more energy and spent more time than me debunking Joy's claims and this is Richard Gill

and the physics community owes him a debt of gratitude for putting this nonsense to rest. There were also two good things coming out of this challenge to Bell's theorem.

First, Sascha Vongehr came with what he called a Quantum Randi Challenge: show you beat Bell's theorem on a computer or shut up. With programming help from Cristi Stoica I came up with this simple Java Script program which runs in any web browser which anyone can use to try to disprove Bell's theorem until they really understand why it is an impossible task.

Second, James Owen Weatherall actually manage to fulfill Joy's hope to eliminate the extra term in a mathematically valid model which was not using Clifford algebras. But then would this count as a "disproof" of Bell's theorem? NO because the actual experimental outcomes are +1 and -1 and the correlations must be computed using them and not in a space of make-believe statistics. 

So even if Joy's math were valid, it would not represent in any way a "disproof" of Bell's theorem. 

Now what I found completely amazing was that after resigning his FQXi membership Joy received encouragements to continue the fight. It is not clear what fight. The fight to prove +1 = -1? Didn't I say soap opera?

Post Script: In case anyone has questions regarding any past or present mathematical, physical, or philosophical claims by Joy, feel free to ask here and I will answer. 
Post Post Script: in an online reply at Sci.Physics.Foundations, Joy claims his model it is not about the sign of sqrt(-1). Oh yes it is, by Hodge duality. And Joy knows that because he used to call the two Hodge duality for distinct Clifford algebras "Joy duality" which earned him high marks in his crackpot index for naming equations after yourself. The moderator of that blog, FreddyFizzx is in cahoots with Joy to promote Joy's ideas and suppress sane opposite points of view.